رياضيات تطبيقيةرياضيات جامعي
صياغة النموذج الرياضي لمشكلة البرمجة الخطية
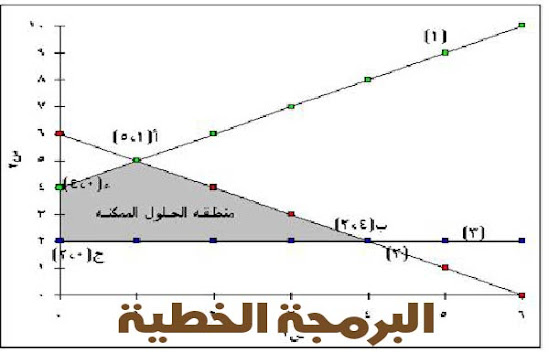
صياغة النموذج الرياضي لمسألة البرمجة الخطية
مقدمة
من المعلوم أن البرمجة الرياضية تعتبر أحد الأساليب الرياضية (الكمية) للتخطيط ، والذي يساعد صانع القرار على إتخاذ القرار الأمثل فيما يتعلق بتعظيم الارباح أو تقليل الخسائر لمنشأة ما ، في ظل الموارد المتاحة ، و يتم التوصل إلى الحل الأمثل من خلال صياغة نموذج رياضي (معادلات او متراجحات أو كليهما) يعبر عن وضع المنشأة وإمكانياتها ، ثم حل هذا النموذج .
ويتكون النموذج الرياضي من مجموعة من المعادلات أو المتراجحات أو كليهما تعبر عن الموارد المتاحة تسمى القيود ، و دالة تعبر عن الهدف من البرمجة تسمى دالة الهدف ، و دالة الهدف إما أن تكون من النوع تعظيم ( تكبير الأرباح) او تصغير ( تقليل الخسائر) ، وإذا كانت جميع المعادلات و المتراجحات الداخلة في تركيب النموذج من الدرجة الإولى (اي أس كل متغير يساوي واحد ) فإن النموذج الرياضي يسمى نموذج خطي و البرمجة تسمى برمجة خطية وهي موضوع مقالتنا هذه .
خطوات صياغة النموذج الرياضي
1- تحديد متغيرات النموذج و التعبير عنها برموز رياضية.
2- ترجمة الموارد المتاحة الى معادلات أو متراجحات رياضية.
3- ترجمة هدف صانع القرار الى دالة رياضية.
مثال توضيحي
مصنع ينتج طاولات و كراسي على مرحلتين المرحلة الأولى مرحلة تقطيع الخشب و المرحلة الثانية مرحلة التجميع والتركيب و تحتاج الطاولة الى 4 ساعات في مرحلة التقطيع و ساعتين في مرحلة التجميع ، بينما يحتاج الكرسي الى ساعتين في مرحلة التقطيع و 4 ساعات في مرحلة التجميع ، فإذا كان ربح المصنع من الطاولة 8 دولار و من الكرسي 6 دولار ، فما هو العدد الأمثل من الطاولات و الكراسي الذي يجب على المصنع أن ينتجها في الإسبوع لكي يحقق اكبر ربح ممكن ؟ إذا عُلم أن الطاقة القصوى للمصنع هي 60 ساعة في الإسبوع في مرحلة التقطيع و 48 ساعة في مرحلة التجميع.
المطلوب : صياغة النموذج الرياضي للبرمجة الخطية لهذه المسألة.
نتبع الخطوات التالية :
1- تحديد متغيرات النموذج : من الواضح أن المتغيرات التي نرغب في تحديد أفضل القيم لها للحصول على اكبر قدر ممكن من الارباح هي عدد الطاولات و عدد الكراسي و سنرمز لعدد الطاولات بالرمز B و عدد الكراسي بالرمز T.
2- ترجمة الموارد المتاحة الى لغة الرياضيات : كون كل طاولة تحتاج الى 4 ساعات في مرحلة التقطيع ، فإن عدد الساعات التي نحتاجها لجميع الطاولات هي 4B في مرحلة التقطيع ، وبالمثل عدد الساعات التي نحتاجها لجميع الكراسي 2T في مرحلة التقطيع ، و بالتالي عدد الساعات التي نحتاجها للطاولات و الكراسي معاً في مرحلة التقطيع هو 4B + 2T و بما أن الطاقة القصوى للمصنع هي 60 ساعة فقط في مرحلة التقطيع ، فهذا يعني أنه يجب أن يكون 4B + 2T <= 60 ( الرمز => يعني اصغر من او يساوي ) ، وهذا هو القيد الاول .
و كون كل طاولة تحتاج الى 2 ساعة في مرحلة التجميع ، فإن عدد الساعات التي نحتاجها لجميع الطاولات هي 2B في مرحلة التجميع ، وبالمثل عدد الساعات التي نحتاجها لجميع الكراسي 4T في مرحلة التجميع ، و بالتالي عدد الساعات التي نحتاجها للطاولات و الكراسي معاً في مرحلة التجميع هو 2B + 4T و بما أن الطاقة القصوى للمصنع هي 48 ساعة فقط في مرحلة التجميع ، فهذا يعني أنه يجب أن يكون 2B + 4T <= 48 ، وهذا هو القيد الثاني.
3- صياغة دالة الهدف : هدف المصنع هو الحصول على أكبر قدر ممكن من الأرباح ، سنرمز للأرباح بالرمز Z ، وبما أن ربح كل طاولة 8 دولار فيكون ربح جميع الطاولات 8B ، وبالمثل يكون ربح كل الكراسي 6T ، وبالتالي ربح الطاولات و الكراسي معاً 8B + 6T ، إذن دالة الهدف هي :
Z = 8B + 6T
إذن سيكون النموذج الرياضي لهذه المسألة كما يلي :
و كلمة Maximize بجوار دالة الهدف تعني أن دالة الهدف من النوع تعظيم و ليس تصغير ، أي أن المطلوب أكبر قيمة لـ Z بدلالة B و T.
***********************
***********************




ليست هناك تعليقات:
إرسال تعليق